Планирование эксперимента
Зачем нам модель и что это такое? Этот вопрос, к сожалению, возникает в головах специалистов по качеству достаточно редко. Моделирование относится к достаточно сложным методам. Но сложность обманчива и с лихвой окупается получаемыми с помощью моделей результатами.
С помощью моделей (особенно в процессах со многими входными параметрами, когда нельзя представить зависимости показателя качества от этих параметров графически) можно легко проигнорировать значение получающегося качества процесса или продукта при тех или иных условиях, можно организовать поиск наилучших (оптимальных) условий проведения процесса чтобы снизить затраты, повысить потребительские свойства продукта или полуфабриката, повысить производительность и решить ряд других задач по улучшению качества процессов.
Математическое моделирование как инструмент познания завоевывает все новые и новые позиции в различных областях деятельности человека. Оно становится главенствующим направлением в проектировании и исследовании новых систем, анализе свойств существующих систем, выборе и обосновании оптимальных условий их функционирования и т.п. Математическое моделирование широко проникло в различные области знаний и их приложения: технические, экономические, социальные, биологические и многие другие на первый взгляд далекие от математики. Поэтому специалистам необходимо владеть концепциями и методами математического моделирования, иметь представление об инструментарии, применяемом при моделировании.
Данный раздел посвящен вопросам построения регрессионных моделей - уравнений связи различных входных факторов (параметров процессов, оборудования, состава смеси и пр.) с выходными (производительность, различные показатели качества процесса, продукта и пр.) и планирования экспериментов для облегчения построения моделей. Специальная организация исследований позволяет с минимальными для заданного числа экспериментов затратами получить необходимую о процессе информацию.
В программе рассмотрены способы планирования, реализации и обработки результатов для общего подхода построения моделей (регрессионный анализ), полного факторного эксперимента (ПФЭ), дробного факторного эксперимента (ДФЭ), ортогонального и центрального композиционного плана второго порядка (ОЦКП).
Доступные версии программы:
![]() 1.0.10.6
Скачать дистрибутив
1.0.10.6
Скачать дистрибутив
![]() 1.0.10.5
Скачать дистрибутив
1.0.10.5
Скачать дистрибутив
![]() 1.0.10.4
Скачать дистрибутив
1.0.10.4
Скачать дистрибутив
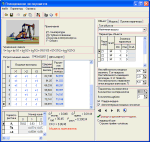
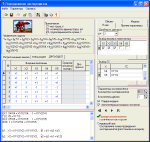
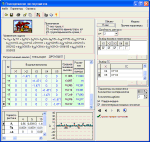
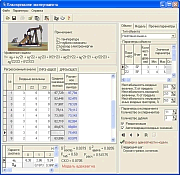
Примеры экранных форм программы:
Системные требования:
Цена: